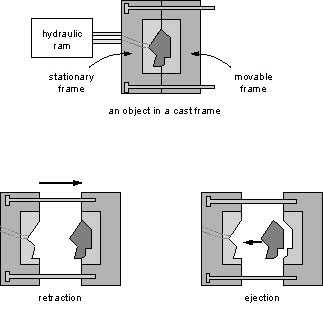
The process of casting in real world
Casting
Geometric Aspects of the Casting Process
Manufacturing is the process of converting raw materials (such as iron, glass or polymer) to useful products, ranging from goods such as kettles and telephones to machinery such as railway locomotives and aircrafts. By means of computer-aided design (CAD) and computer-aided manufacturing (CAM), these manufacturing processes have been done in a form of automation, both in design phase and construction phase. Due to the geometric nature of manufacturing processes, many geometric problems has arised in it. Computational geometry arises at all levels of manufacturing, from design, modeling and simulation, to process planning, on-line verification and testing.
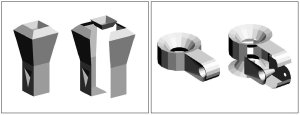
In casting, liquid is poured into a cast that has a cavity with the shape of the object to be manufactured. The liquid then hardens, after which the cast is removed and one is left with an object whose shape is that of the cavity. The key property necessay for casting is that the cast parts can be removed from the object without destroying either the cast parts or the object. This ensures that the given object can be mass produced by re-using the same cast parts.
Papers published or submitted for publication
Separating an Object from its Cast
We consider the case where the cast consists of two parts and address the following problems.
(1) Given a cast for an object and a direction d, can the cast be partitioned into two parts
such that the parts can be removed in directions d and -d, respectively, without colliding
with the object or the other cast part? (2) How can one find a direction d such that
the above cast partitioning can be done? We give necessary and sufficient conditions for both
problems, as well as algorithms to decide them for polyhedral objects.
with Mark de Berg, Prosenjit Bose, Siu-Wing
Cheng, Dan Halperin, Jirí Matousek, and Otfried Schwarzkopf
In Proc. 13th Annu. ACM Symposium on Computational
Geometry, 221--230, 1997 and in
Computer-Aided Design, 34(8):547-559,
2002

Casting with Skewed Ejection Directions
We
give necessary and sufficient conditions to test the feasibility of
the cast part retraction and object ejection, where retraction and
ejection directions need not be the same. For polyhedral objects,
we show that the test can be performed in O(n^2\log^2 n) time and
the cast parts can be constructed within the same time bound. The
complexity of the cast parts constructed is worst-case optimal. We
also give a polynomial time algorithm for finding a feasible pair of
retraction and ejection directions for a given polyhedral object.
with Siu-Wing Cheng, and Otfried Cheong
In Proc. 9th Annu. International Symposium on Algorithms and
Computation, 1998, and in
Algorithmica, 44(4):325-342, 2006
Casting with Directional Uncertainty
We consider directional uncertainty: given a 3-dimensional polyhedral object, is there
a polyhedral cast such that its two parts can be removed in opposite directions
with uncertainty \alpha without inflicting damage to the object or the cast
parts? We give a necessary and sufficient condition for castability, and a randomized algorithm
that verifies castability and produces two polyhedral cast parts for a polyhedral object of
arbitrary genus. Its expected running time is O(n\log n). The resulting cast parts
have O(n) vertices in total. We also consider the case where the removal direction
is not specified in advance, and give an algorithm that finds all feasible removal directions
with uncertainty \alpha in expected time O(n^2\log n/\alpha^2).
with Otfried Cheong, and René van Oostrum
In Proc. 13th Annu. International Symposium on Algorithms and
Computation, 2002, and in Computational Geometry: Theory and Applications,
26(2):129-141,
2003
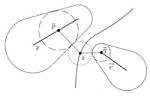
The Reflex-Free Hull
We propose a hull operator, the reflex-free hull, that allows us to
define a 3D analogue to bays in polygons. The reflex-free hull allows a rich
set of topological types, yet for polyhedral input with $n$ edges, it remains
a polyhedral set with O(n) edges. This is in contrast to other possible
hull definitions that give non-planar surfaces and higher combinatorial
complexity. The reflex-free hull is related to identifying cavities in
computer aided design and manufacturing, but we sketch examples to indicate
that computing a reflex-free hull will be a challenging problem.
with Siu-Wing Cheng, Otfried Cheong, and Jack Snoeyink
In Proc. 13th Canadian Conference on Computational
Geometry, 2001, and in International Journal of Computational Geometry and Applications,
14(6):453-474, 2004

Casting an Object with a Core
This
paper addresses geometric problems that concern manufacturing an
object using a cast with a core. In casting, molten material
is poured into the cavity of the cast and allowed to solidify. The
cast has two main parts to be removed in opposite parting directions.
To manufacture more complicated objects, the cast may also
have a core to be removed in a direction skewed to the parting directions.
In
this paper, given an object and the parting and core directions,
we give necessary and sufficient conditions to verify whether a
cast can be constructed for these directions. In the case
of polyhedral objects, we develop a discrete algorithm to perform
the test in $O(n^3\log n)$ time, where $n$ is the object size. If
the test result is positive, a cast with complexity $O(n^3)$ can
be constructed within the same time bound. We also present
an example to show that a cast may have $\Theta(n^3)$ complexity
in the worst case. Thus, the complexity of our cast is worst-case
optimal.
with Sang-Won Bae, Siu-Wing Cheng, and
Kyung-Yong Chwa
In Proc. 16th Annual International Symposium
on Algorithms and Computation 2005. To appear in Algorithmica.
More details available [ PDF]
My thesisis available [ online]